Beiträge von inkman

Gelegentlich werden Skalenserien als besonders infrarot-reaktiv beworben. Auch unter den Bindemitteln gibt es diese Argumentation - meist gerichtet an Farbhersteller.

Die Anbieter wollen besonders hervorheben, dass eine Farbe, die von sich aus schon schnell wegschlägt, durch die Erwärmung besonders beschleunigt werde. Dies wird als eigenes Trocknungskonzept dargestellt, was fachlich gesehen, Unsinn ist. Werblich ist es aber gut verwendbar, weil es so plausibel klingt. Und es rückt diese Farben in eine Nähe zu den UV - Farben, macht aus ihnen also eine technologische Besonderheit. Als sei das ein Prinzip der Strahlenhärtung.

Dass auch noch heute frisch aufgelegte Fachbücher ihren Lesern diesen alten Bären aufbinden, deutet nur darauf hin, dass man als Autor gut schauen sollte, womit man Weisheit verbreitet - und wobei man Unverstandenes nachplappert.

Das war einmal generell so und gilt auch heute noch für viele Digitaldrucker. Inzwischen haben sich aber die unterschiedlichen digitalen Techniken in eigene Richtungen entwickelt und teilweise ganz eigene Stärken entwickelt.

Die Tonerverfahren (elektrofotografisch) übertragen Schichtstärken um 20 µm, haben inzwischen auch so etwas wie Lackierungen dabei. Das führt sie in ganz andere Zielgebiete aus dem Offset mit seinen 1 µm hinaus. Flüssigtoner (Indigo) können sogar sauberere Rasterstrukturen erzeugen als der Bogenoffset.

Trotzdem hält sich das Vorurteil, und einige Geräte imitieren sogar die Rasterrosette, um den Offset zu kopieren, eher doch ein Qualitätsnachteil.

Der Ink Jet schwingt sich in noch ganz andere Höhen. Einerseits simulieren Ink Jet Proofer in akzeptabler Weise den Offsetdruck bis hin zur Farb- und Rasterverbindlichkeit. Andererseits schaffen dicke UV - Lack - Schichten im Ink Jet auf riesigen Plakaten einen Lichtschutz für den Druck mit Standzeiten von einem ganzen Jahr und mehr. Davon träumt der Offset vergeblich...

Füllstoffe und Pigmente sind in der Technik mikrokristalline Stoffe, die sich typischerweise im Anwendungsmedium nicht lösen, sondern kristallin bleiben.

Der Übergang vom reinen Verbilliger (Füllstoff wird neudeutsch auch Extender genannt) zur funktionellen Rezeptkomponente ist fließend.

In Druckfarben bezeichnen wir die ungefärbten Mittel als Füllstoffe, die farbigen als Pigmente. Farbe ist dabei auch Schwarz (Ruß) oder Deckvermögen (Deckweiß).

Pigmente sind also Farbmittel. Füllstoffe setzt man ein, um einer Farbe oder einer Paste ein bestimmtes rheologisches Profil zu vermitteln, also z. B. die Viskosität zu stützen.

Füllstoffe in Druckfarben kommen meist aus dem Bereich der anorganischen Chemie (Kieselsäure, Kalkstein, Kreide, Dolomitmehl, Bentonite, Montmorilllonite), Pigmente dagegen weitgehend aus der organischen. Eines der wenigen anorganischen Pigmente ist z. B. Titandioxid, durchweg in seiner Form als Rutil wegen dessen Brechkraft.

Man kann rheologische Eigenschaften auch mit anderen Mitteln steuern, z. B. durch Gelierungen im Bindemittel oder partielle Polymerisation von Rezeptkomponenten wie bei den Oligomeren im UV-Bindemittel. Dieser Weg ist aber nur für einen Anteil der rheologischen Forderungen nutzbar. Füllstoffe sind oft unumgänglich - und meist auch relativ kostengünstig.

Eine einfache Darstellung: Eine Farbe ohne Pigment nennen wir Lack. Haben wir anstelle der Pigmente Füllstoffe, so tritt das ganze Ding auf wie eine Farbe, färbt nur praktisch nicht, z. B. ein Mischweiß.

Allgemein kann man sagen, dass fast jedes Papier und jeder Karton im Offset bedruckt werden kann - wenn es / er nicht zu rupfempfindlich ist. Es ist also nicht sinnvoll, Tissue - Papiere oder Bierdeckelkarton aus dem Flexo herauszuholen. Man müsste die Farben und vermutlich auch die Maschinenführung sehr weit an solche weichen Bedruckstoffe anpassen.

Offsetfarbe haftete auf praktisch allem, weil sie ja hauptsächlich disperse Oberflächenverhältnisse anbietet (also wenig polare).

Bei der oxidativen Verfilmung (Trocknung) gibt es allerdings ein paar Bedenken. So ist Transparentpapier, BOPP - Folie und auch PE-extrudierter Karton eine Sache nur für ausgefuchste Spezialisten.

Anders verhält es sich bei den diversen Digitaldrucktechniken. Pudertoner scheinen hier auch weniger empfindlich zu sein. Dennoch weiß man in manchem Büro, dass der Laserdrucker auf bestimmten Papierqualitäten besser ausdruckt als auf anderen.

Flüssigtoner (z. B. Indigo) benetzt nicht alle Papiere wirklich gut. Hier kann der Papierlieferant helfen.

Mit dem Inkjet verhält es sich ganz speziell, weil mittlerweile besondere Beschichtungen das Verlaufen der Tröpfchen und ihre Trocknung gezielt unterstützen. Man sollte bei gehobener Druckqualität darauf achten, ob der Hersteller diese Bedruckbarkeit garantiert. Gerade hier sind ein Test oder die Beschränkung auf geprüfte Qualitäten wichtig.

Die Lichtechtheit der Drucke sollte mindestens WS 4 betragen, besser 5, weil ein ganzer Monat am Licht schon anspruchsvoll sein kann. Das wird bei Sonderfarben manchmal übersehen. Und nicht immer wird berücksichtigt, dass die Lichtechtheit, die auf der Dose steht, nur für Normdrucke gilt. Die haben eine Farbschicht von 1,5 g/m². Praxisdrucke liegen nur bei 0,7 bis 1,2 g/m². Und wo weniger Material liegt, ist es schneller vom Licht zerschossen.

Manche Kalender haben um ein zentrales, großes Bild einen Rahmen, ein Passepartout. So etwas kann besonders in kräftigen und gebrochenen Farbtönen wie eine Schablonier - Testform wirken.

Die Tinten und Druckfarben für den Inkjet enthalten Wasser oder Lösemittel als Flüssigkomponenten. Das bedeutet, dass wegschlagende und verdunstende Trocknung als Mechanismus vorherrschen. Häufig werden Papiere mit ganz speziell angepassten Oberflächen (Porosität) eingesetzt, die die Tröpfchen fixieren helfen, bevor sie zerfließen. Damit ermöglichen sie winzigste Tröpfchengrößen, also feinste Zeichnungselemente (neudeutsch "Pixel").

Strahlenhärtende Farben finden wir besonders im großformatigen Inkjet (large format printing), deren Bindemittel durch z. B. UV-Licht über eine Polymerisation aushärten. Sie ermöglichen die Bedruckung von speziellen Bedruckstoffen wie Kunststoffen (Schilder, Planen) und Textilien.

Der korrekte Name ist übrigens "spezifische elektrische Leitfähigkeit", gemessen in mSiem/cm.

Auch wenn eine halbwegs genaue Angabe nur mit Originalsubstanzen ermittelt werden kann, kann man doch grobe Grenzen formulieren und mögliche Risiken für Fälle nennen, in denen sie überschritten werden.

Messungen sollten bei 20 °C vorgenommen werden - oder wenigstens darauf umgerechnet. Hierbei hat sich ein Gefälle von 2,5 % pro Grad Temperaturdifferenz praktisch bewährt. Das bedeutet, dass ein Leitwert mit jedem Grad wärmer um 2,5 % steigt.

Liegt man bei einem Maschinenwasser unter 1000 µSiem/cm, besteht die Gefahr, dass nicht genügend Puffersalze vorliegen. Dann kontrolliert man den pH. Und solange der im Soll bleibt, ist auch alles in Ordnung. Erst wenn er steigt, sollte man etwas mehr Konzentrat (1 %) zugeben.

Liegt er aber über 3000 µSiem/cm, dann ist das kein Feuchtmittel mehr, sondern eine Salzlorke. Darin zersetzen sich flott die Oktoate, die eigentlich die oxidative Verfilmung beschleunigen sollen. Die Farben werden also nur sehr langsam oder gar nicht mehr fest. Hier hilft nur sofortiger Austausch des gesamten Feuchtmittels. Dies gilt allerdings nur, wenn man wirklich oxidative Verfilmung benutzt, also z. B. im Standardfall des Bogenoffsets. Im Coldset und in den meisten Heatset-Fällen gibt es keine Sikkative, also auch kein Verfilmungsrisiko. Dann ist der Leitwert etwas lockerer zu sehen und kann eher auf Emulgier-Risiken hinweisen, wenn er viel zu hoch ist. Ob hier allerdings die 3000 mSiem/cm-Fausregel gilt, weiß ich nicht sicher genug, weil ich diese Fälle nicht aus eigener Praxis kenne.

Wenn bunte Bilder, also Rasterdrucke mit den Skalenfarben, nachträglich veredelt werden, kann es in unterschiedlichen Bildpartien zu unterschiedlichen Farbveränderungen kommen. Dann kann das in strengen Fällen zu Reklamationen führen, obwohl der Drucker seine Auflage sehr genau nach Vorlage gedruckt hat. Hier sind noch nicht einmal die Farbveränderungen durch Wegschlagen gemeint, weil die bei den nicht ganz so hoch pigmentierten Skalenfarben nicht ins Gewicht fallen.

Allein eine transparente Schicht auf dem getrockneten Druck verändert die farbliche Wirkung der drei Buntfarben unterschiedlich. Schwarz, Cyan und Magenta scheinen tiefer und klarer - farbstärker. Bei Gelb merkt man nicht viel, weil es als helle Farbe visuell einen geringeren Einfluss hat.

Anfänglich haben wir einen „Lupeneffekt“ gesucht. Inzwischen ist aber ziemlich klar, dass es sich um eine Mischung aus bekannten Effekten handelt: Der Druck verliert bei der Kaschierung oder Lackierung seine oberflächliche Lichtstreuung, die ja immer etwas flau macht und vergraut. Außerdem wird ein eventueller Bronzeeffekt, besonders beim geschönten Schwarz, unterdrückt. So kann es geschehen, dass sehr unbunte Partien einen leichten Farbstich bekommen. Und kräftig bunte Partien treten mit ihrem Hauptanteil von Cyan oder Magenta hervor - je nachdem, welche dominiert.

Dann kann in einem Bild mal ein Bereich zu grün und ein anderer zu rot sein.

Meist wird es bei Skalendrucken mit den Farbtönen ja nicht so genau genommen. Aber es kann bei Markenwerbung oder - eben - unbunten Partien (z. B. Porzellanabbildungen) schon mal zur Reklamation kommen.

Dieses Problem ist allerdings heutzutage viel geringer als früher, weil auch im Akzidenzbereich immer mehr un-line-Lackierungen auftreten. Da sieht der Drucker ja sein Ergebnis sofort aus der Maschine.

Jeder von uns kennt das „1 part per million“, also ein Millionstel.

Das redet sich einfach und taucht oft in Grenzwert – Beschreibungen auf. Unsere chemische Analytik reicht inzwischen in vielen Bereichen so weit hinunter, dass sie sogar die „Allgegenwarts-Konzentration“ mancher Substanzen zahlenmäßig erfasst. Aber welche Vorstellung können wir uns vom ppm machen, um nicht laienhaft einfach nur Zahlen zu plappern?

Einen guten Ansatz findet man in Gießen. Da ist ein Museum, das „Mathematikum“. Nicht erschrecken, es ist ein Museum für Kinder und neugierig gebliebene Erwachsene, in dem mathematische Begriffe und Zahlen so verdeutlicht werden, das sie jeder begreift. Und ppm zeigen sie dort so: In einer Glastrommel von geschätzt 30 cm Durchmesser und 1 m Länge befinden sich 1 Million Glaskügelchen. Alle Kügelchen sind glasig farblos – bis auf eine. Die ist schwarz. Und man kann so lange drehen, bis man die kleine schwarze erkennt. Nicht bei jeder Umdrehung kommt sie nach oben.

Die zweite Interpretation habe ich von einem Freund aus dem Siegwerk: Ein Preuße (Berliner) pro München ist ein ppm unter Bayern.

In der chemischen Analytik und den Diskussionen über Grenzwerte werden sogar ppbs bemüht, parts per billion, also Teile pro Milliarde. Das bedeutet so etwas wie 1,5 europäische Touristen als einzige in Indien. Ob alle Journalisten, die solche Zahlen verwenden, auch nur eine Spur von Ahnung haben, was sie sagen?

Ich will ausdrücklich sagen, dass diese analytische Schärfe ein fantastischer Fortschritt unserer Technik ist. Angemessener Umgang ist mein Punkt.

Die Ursprünge unserer modernen Messtechnik liegen in den Anwendungen und Bedürfnissen des Buchdruckes, denke ich. An seinen Druckmaschinen konnte man zonal die Farbschichtdicke auf den Walzen regeln und brauchte dafür eine griffige Messgröße.

Die optische Wirkung einer bedruckten Fläche liegt in der Lichtabsorption. Versuchen wir es also mal mit der Absorption.

Ohne Einfärbung ist sie gleich Null, mit mehr und mehr Farbe steigt sie. Das ist schon besser als bei der Remission, denn die ist ohne Farbe am höchsten und sinkt bei sehr, sehr dicker Farbschicht auf Null.

Aber wenn wir die Absorption mal quantitativ (mengenorientiert) betrachten, sieht es wieder wenig praktisch aus. Der Grund ist einfach im Modell mehrerer einzelner Farbschichten übereinander zu zeigen: Nehmen wir an, die erste Schicht schwächt das Licht auf die Hälfte. Die zweite Schicht schwächt diese wieder auf ihre Hälfte, also um ein Viertel der ursprünglichen Stärke. Das geht so weiter, ein Achtel, ein Sechzehntel usw.

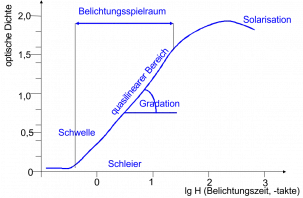
Praktisch wäre ein Maß, das bei der doppelten Farbschicht auch einen - wenigstens ungefähr - doppelten Messwert zeigt. Damit wären wir beim Vorschlag der optischen Dichte, der aus der Vorstufe mit fotografischen Filmen als Maß für Schwärzung bekannt war. Man musste sie nur auf klare Wellenlängenbereiche definieren, damit man Cyan, Magenta und Yellow einzeln erfassen konnte. Dafür die Farbfilter.

Außerdem haben wir ja Auflicht - Verhältnisse. Da interessiert uns wenig, wie viel die Lampe denn abgibt, das I₀ vom Durchlicht. Wir hätten lieber einen Vergleich mit dem, was eine Blanko-Fläche zurückwirft. Das wäre unser „100%“. Wir brauchen also aus aus dem Techniker-Vokabular einen „Remissiongrad“ (s. a. Quizfrage 198):

Lichtströme zurückgegeben

I_Druck vom Druck

I_blanko vom Blankopapier

Weil ich es gerade nicht besser kann, schreibe ich hier "Beta" für den griechischen kleinen Buchstaben, den man üblicherweise hier nimmt.

Remissionsgrad

Beta = I_Druck / I_blanko

Wir übernehmen die optische Dichte mit dem Logarithmus des Transmissionsgrades und ersetzen ihn durch unseren technischen Remissionsgrad.

optische Dichte im Druck

D = - log Beta = log ( I_blanko / I_{Druck )}

Das ergibt eine Kurve, die bei I_Druck = I_blanko von 0 startet (Logarithmus von 1), ziemlich gerade (quasilinear) ansteigt und erst in höheren Bereichen (über 5) mit der Krümmung beginnt.

Interessant ist noch, dass die optische Dichte eine reine Logarithmenzahl ist, also keine Dimension wie m, sec oder g hat.

(s. a. Frage 127: Wellenlängen bei opt. Dichte)

Auch wenn viele Praktiker Physik und Chemie nicht schätzen, leisten sie uns doch gerade in der Praxis gute Dienste. Wenn wir einfache Darstellungen aussuchen, haben wir auch mehr Nutzen als Aufwand. Der Vorteil an wissenschaftlichen Beschreibungen ist, dass die Ausdrücke exakt definiert werden und dann auch exakt zu verstehen sind. Wir müssen sie eben nur nicht mit gleichlautenden Ausdrücken aus der Umgangssprache verwechseln.

Die Physik bietet uns drei Ausdrücke an:

1. Absorption,

2. Reflexion und

3. Transmission.

Absorption will das geschluckte Licht benennen, Reflexion das zurückgeworfene und Transmission das hindurchgelassene.

Mit einem Photometer können wir die Stärke von Lichtstrahlen messen. Wir halten es direkt in den Strahlengang einer Lampe und messen I_0. Dann prüfen wir ebenso, ob etwas zurückgeschickt (I_refl, reflektiert) oder hindurchgelassen wird (I_trans, transmittiert). Wenn die beiden I_refl, und I_trans zusammen weniger ergeben als das drauf gestrahlte I₀, dann muss die Differenz natürlich I_abs (absorbiertes Licht) sein. So misst man das.

Die 3 Strahlen - Anteile bezieht man auf den eingestrahlten Ursprungsstrahl und definiert die Bruchteile:

Das ist die Version der Physiker. Die Formeln und die Symbole brauchen wir nicht unbedingt in unserer Praxis, wenn wir damit Schwierigkeiten haben. Die drei Begriffe sind aber schon wichtig auch für uns. Hierbei spielt der Transmissionsgrad klar seine Rolle beim Film und der Durchlicht - Densitometrie. Der Reflexionsgrad - oder sein technisches Pendant Remissionsgrad - spielen dagegen eine Rolle bei Auflicht-Messungen, dem gängigen Fall unserer Praxis.

In der Technik haben unsere Alten noch einen Begriff definiert, der mit der Reflexion (zurückgebogenes Licht) zu tun hat. Es ist die Remission, also das zurückgeschickte Licht. Der Name sagt nicht, warum sie da ist. Und der Unterschied ist fein: „Reflexionsgrad“ bezieht das zurückgegebene Licht auf die Stärke des eingestrahlten. „Remissionsgrad“ dagegen bezieht das zurückgegebene Licht auf das, was ein sehr weißer Normkörper (Kachel oder Pulverpille) zurückgeben würde. Es liegt auf der Hand, dass die extra Definition aus irgendwelchen messtechnischen Gründen, vielleicht wegen schwieriger Rechnerei früher, erfunden worden ist. Aber es gibt sie nun mal in der Technik. Vielleicht würde man so etwas heute bei den ganzen eingebauten Computern gar nicht mehr extra definieren.

Der Physiker unterscheidet zwei Reflexionen, gerichtete und diffuse. Die gerichtete ist die aus der Schule mit Spiegeln und Einfallswinkel = Ausfallswinkel. Die diffuse tritt in den Fällen auf, in denen nicht an einer glatten (spiegelnden) Fläche reflektiert wird, sondern an rauen Oberflächen (Papier, Stein...). Physiker betrachten natürlich auch die vielen Fälle der gemischten Erscheinungen und zeichnen dann birnenförmige Verteilungsbilder solcher zurückgeschickten Strahlen (Indikatrix).

Remission hat also ausschließlich mit der diffusen Reflexion zu tun.

Es gibt eine ganze Reihe von Verkrustungen und Ansammlungen von Material, die alle zusammen als Aufbauen bezeichnet werden. Auslöser können alle beteiligten Komponenten sein - Bedruckstoff, Farbe und Feuchtmittel, die Maschine durch Bau und Materialien und nicht zuletzt der Drucker.

Aus dem Papier können Fasern und Strichpartikel heraus gerupft werden und auf Gummi oder Platte kleben bleiben. Dort machen sie Butzen oder die im Kartonbereich bekannten weißen Beläge.

Es kann aber auch subtiler sein, wenn sich z. B. Kalziumkarbonat des Striches im Feuchtmittel auflöst. Dann können sich neue chemische Verbindungen zusammen mit anderen Komponenten formen, z. B. Kalziumzitrat mit dem Puffersystem des Feuchtmittels. Das kristallisiert an Rauigkeiten der Gummiwalzen und macht sie wasserfreundlich - Blanklaufen. Andere Stoffe können ebenfalls selbst oder in Kombination mit Farb- oder Feuchtmittelkomponenten zu chemischen Reaktionen führen, die dann Walzen, Platte, Gummituch belegen und entweder den Farbtransport stören oder gar Krusten bilden.

Farben können unter dem mechanischen Stress der Maschine ihren Zusammenhalt verlieren und eingearbeitete Komponenten absondern. Das typische Beispiel sind Wachse. Man erkennt sie daran, dass sie farblose Schichten auf Walzen, Gummi oder Platte bilden, die beim Darüberreiben glänzend werden. Dann bitte mit einer Klinge abschaben und dem Farb- oder Lackhersteller geben, damit er die Spur verfolgen kann. Auf keinen Fall darf man dann Tesaabzüge nehmen, weil der Klebefilm selbst aus Polyethylen ist und die analytische Erkennung des Polyethylens vom Wachs verhindert.

Bei mechanischem Stress zwischen den Walzen lassen Farben auch ganz andere Dinge fallen; die Palette der möglichen Aufbauursachen ist sehr groß.

Feuchtmittelkonzentrate können zu Plattenverkrustungen auf dem Wege chemischer Reaktionen führen. Und zu guter Letzt kann ein Drucker durch falsche Wasserführung Emulgate unterschiedlichster Art mit unterschiedlichsten Erscheinungsformen produzieren. Oder er kann bei ungünstiger Kombination von Bedruckstoff und Farbe Krusten auf dem Gummi an der Abrisskante von Druckpartien erzeugen.

Für diese Vielfalt könnte man Diagnoseschemata aufstellen, die es erleichtern, Ursachen einzukreisen. Die Fehlerdiagnostik ist ein interessantes Feld, wird allerdings oft durch die Kosten der schadhaften Drucke aus dem technischen in den kommerziellen Diskussionsbereich verschoben. Und dann ist Sachlichkeit nicht mehr einfach.

Der Gammawert eines fotografischen Films beschreibt die Steigung der Schwärzungskurve im linearen Bereich. Er wird auch als Gradation bezeichnet. Eine steile Gradation nennt man auch hart und eine flache weich, weil sich so der Kontrast ergibt.

Ein Bilderfilm - oder auch ein Diafilm - soll möglichst viele verschiedene Halbtöne, im Schwarzweißbild Grautöne, wiedergeben. Dazu muss der Gammawert klein sein, denn dann bildet er durch unterschiedlich viel Licht gut abgestuft unterschiedliche Halbtöne ab. Er hat einen großen Tonwertumfang. In der Praxis liegen Negativfilme etwas über 1, Fotopapiere noch etwas darüber, sodass zusammen 1,5 - 1,6 herauskommen. Beide Verarbeitungsschritte teilen sich also die Beiträge zum Kontrast, und zusammen kommt etwas mehr heraus, als das fotografierte Modell hatte.

Diafilme bringen diesen Kontrast, der einem Gammawert von 1,5 - 1,6 entspricht, gleich in einem Schritt. Das stellt man bitter fest, wenn man von einem Freund ein Dia kopieren möchte und es einfach mit einem normalen Diafilm abfotografiert.

Bei der Reproduktion, im Schritt der Erzeugung einer Druckvorlage, sollen nur zwei Schwärzungsmöglichkeiten benutzt werden, schwarz und transparent beim Film, bei der Platte logischerweise druckend und nicht druckend. Eine sehr steile Gradation des Reprofilms und der Platte kommen dem entgegen. In der Praxis finden sich bei Reprofilmen Gammawerte bis 9.